Quantum walks with dy­nam­ic­al con­trol: graph en­gin­eer­ing, ini­tial state pre­par­a­tion and state trans­fer

Dynamically influencing the walker’s evolution gives a high degree of flexibility for studying various applications. Additionally to the described applications for Anderson localization and percolation we realised time-multiplexed  finite quantum walks of variable size, the preparation of non-localised input states and their dynamical evolution. As a further application, we implement a state transfer scheme for an arbitrary input state to two different output modes.

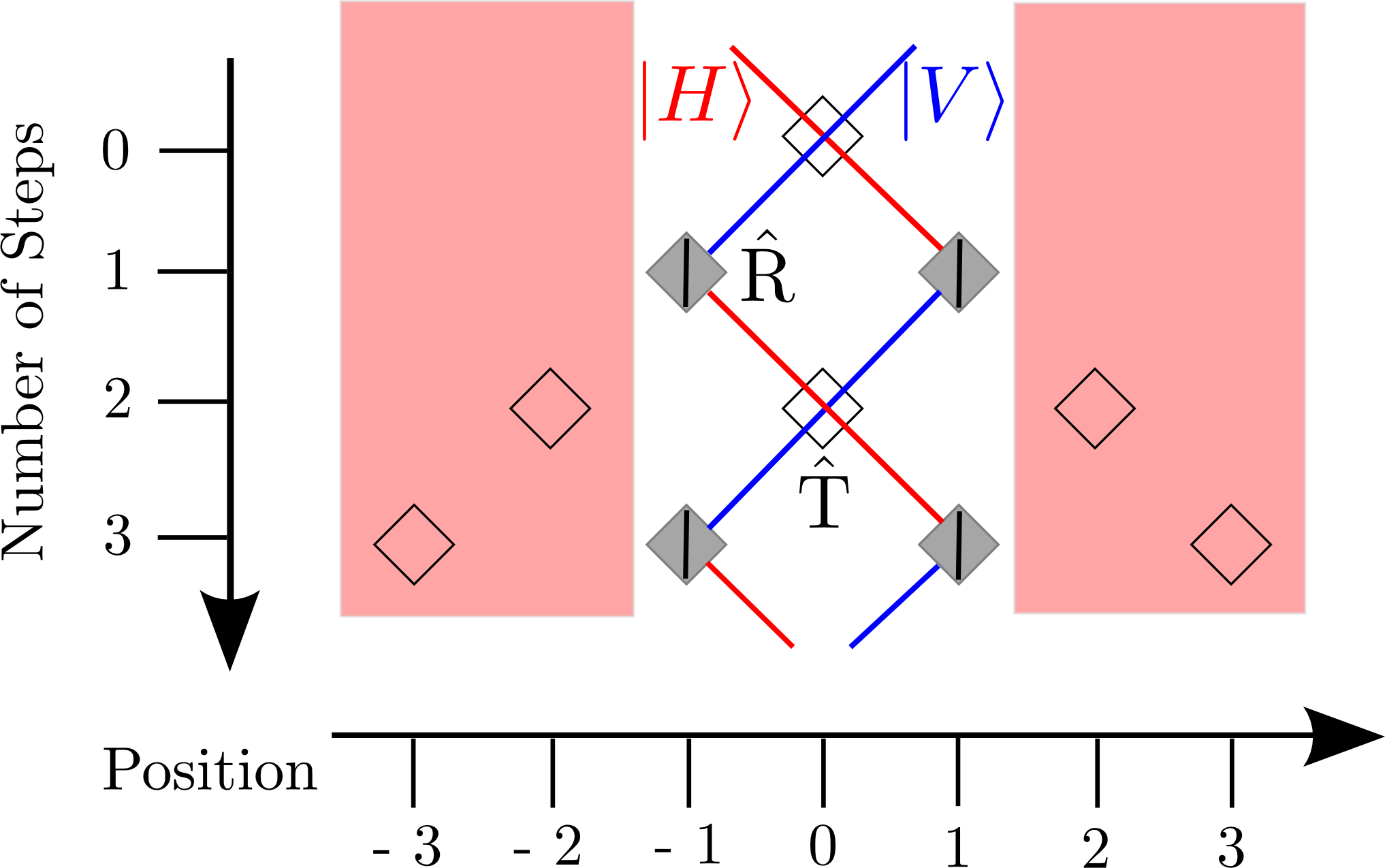
First, we vary the size of the underlying graph by introducing corresponding reflection operations with the EOM as illustrated in fig. 1.

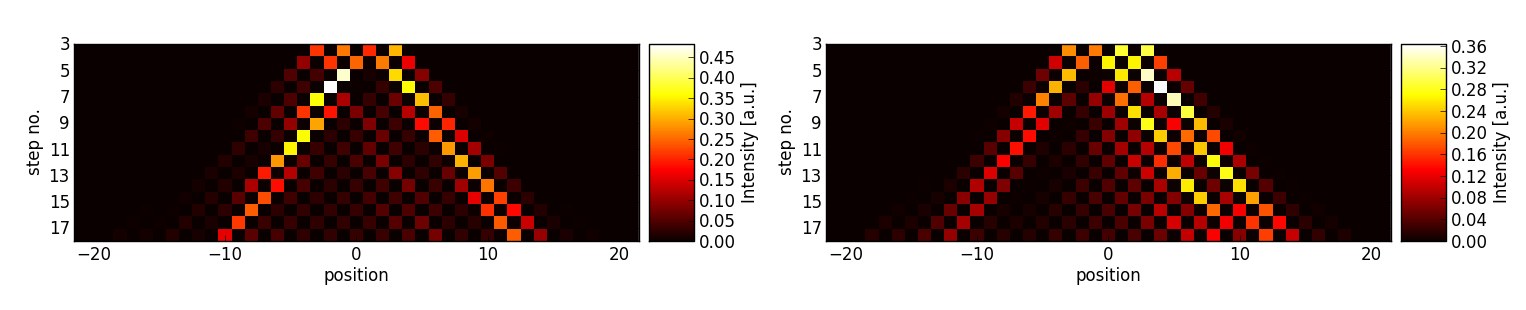
Figure 1: Illustration of how the spread of the walker's external state is limited via polarisation switching; a reflection R is represented by a grey box and switches the horizontal (red lines) into vertical (blue lines) polarization and vice versa. The transmission operation T is represented by a white box leaving the polarizations unchanged. Note that in the setup the spatial position is in the experiment mapped into the time domain. The specific switching pattern determines the size of the underlying graph (here x = {-1,0,1}). Enlarge image

 

The timing of the reflection switching consequently determines how large the graph is and thus how far the walker’s wavefunction is spread out. Three examples for finite graphs in contrast to an unlimited walk are presented in figure 2.

Figure 2: Chessboard representation of the experimental wavefunction of finite walks with a maximum of 4 and 6 simultaneously occupied positions (left and middle) and of an unrestricted (right) walk as comparison; plotted are the steps 1 – 20. Enlarge image

In figure 2a, we observe an additional interesting feature of the walk on a finite graph: The walker, initially spread out, is not only reflected at the boundaries, but even exhibits revival (within experimental errors) at the initial position 0 in step 10.

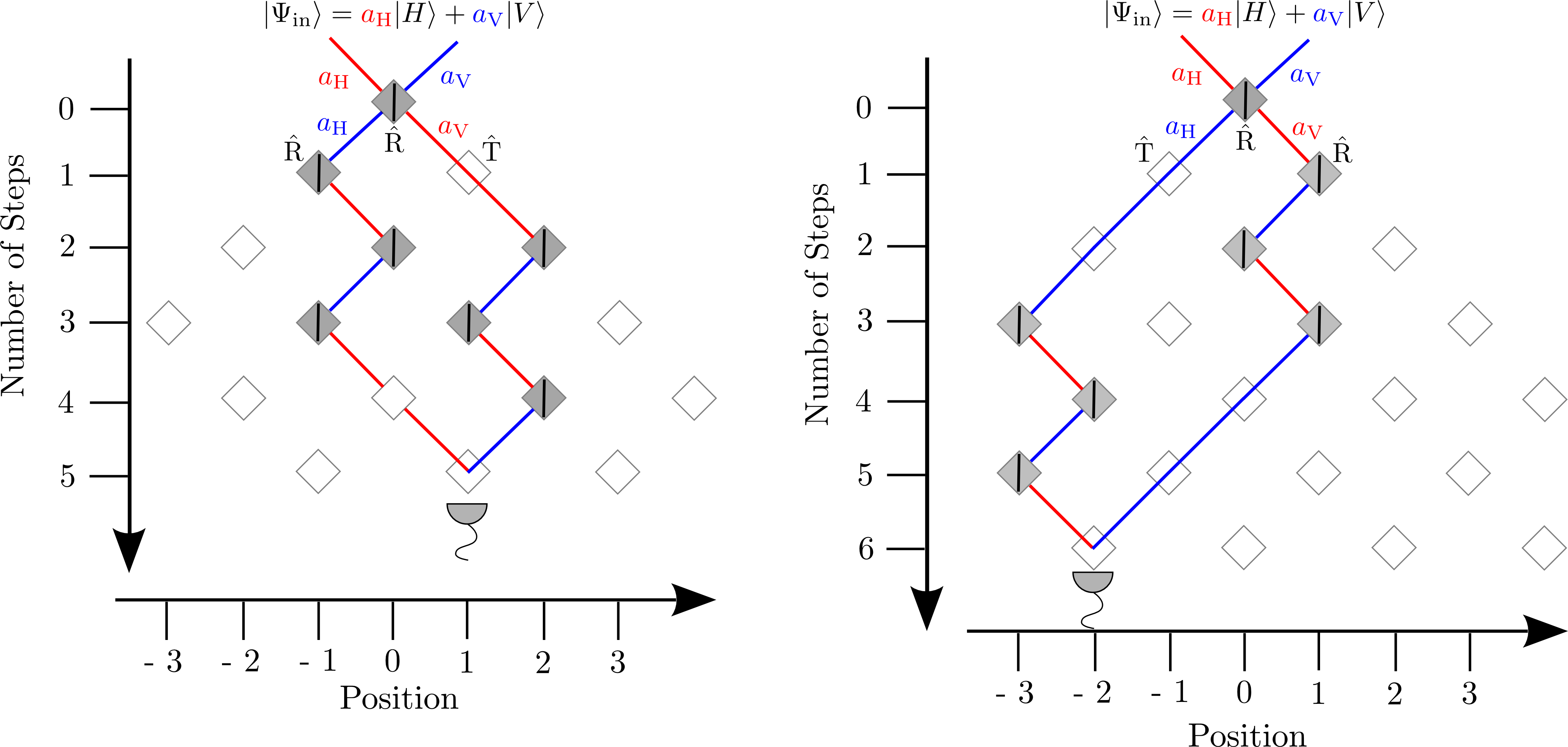
Most quantum walk experiments including those presented above are performed with localised input states. However, there are theory proposals, e.g. for boson sampling in a time-multiplexing setup or for quantum search, which rely on initial states occupying several positions. The ''in-situ'' state preparation, i.e. the preparation of different initial states within the quantum walk setup, guarantees phase-stable pulse trains with controlled polarization inherently exhibiting a coherent evolution. Two examples of transformations accessible by the EOM used in the present setup are illustrated in Figure 3.  We use these schemes to prepare two states with four positions, but different polarizations. 

Figure 3: Illustration of the implementation of the states |VVHH> (left figure) and | VHVH> (right figure) starting from a horizontally polarised input state. C_fair transforms H-polarisation into an equal superposition of H and V. Enlarge image

For these given input states, we observe the evolution in a balanced walk on an infinite graph (see Fig. 4). The comparison of the two cases reveals the relevance of the input polarisation: For the | VVHH> state, the walker evolves along two branches which are more distinctively defined than for the | VHVH>state. Here in comparison, especially the right branch is much more smeared out leading to a very different intensity distribution in position space. By reprogramming the EOM switching patterns, the preparation of well-defined input states distributed over a higher number of positions is possible as well.

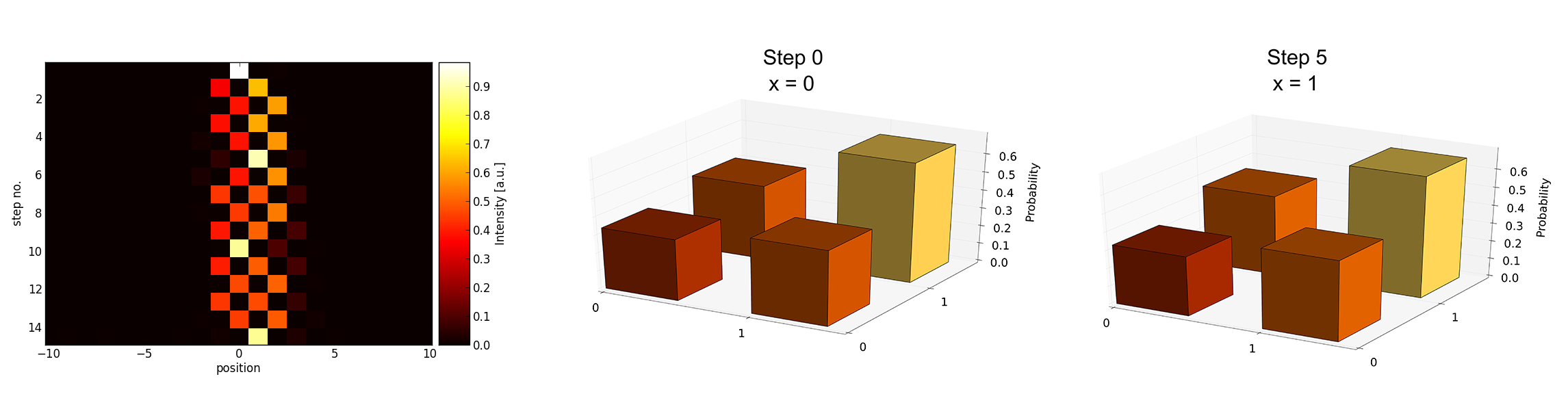
Figure 4: Chessboard representation of the dynamics of the input state |VVHH> (left) and input state| VHVH> (right). Enlarge image

Zhan et al.  in [1] proposed a state transfer scheme via discrete time quantum walks. The possibility of dynamical coin control allows for the easy implementation of this protocol in our setup. We are able to observe a revival of the walker's initial polarisation state at a chosen position, although it is beforehand spread out in space and undergoes switchings in polarization. Different protocols transferring the state to different positions can be realised simply by reprogramming the EOM.  In figure 5, we show the implementation of 2 exemplary non-trivial schemes.

Figure 5: Illustration of the implementation of different possible state transfer schemes: a 5 step state-transfer scheme (left) and a 6 step state-transfer scheme (right). Enlarge image
Figure 6: Left: Intensity distribution of the wavefunction and the absolute values of the density matrix of the polarization of the transferred state in the 0th step at the position x= 0 (middle) and 5th step at the position x= 1 (right) of the 5 step transfer scheme. Enlarge image

All the presented experiments rely on the full dynamical control of the time-multiplexed quantum walk, which includes adjustable coin operation as well as the possibility to flexibly configure the underlying graph structures. Details about the presented applications as well as a thorough explanation of all the experimental challenges and pitfalls including a full analysis of the EOM features, timings and loss handling are published in [2].

 

References:

  1. Zhan, X., Qin, H., Bian, Z., Li, J., Xue, P., 2014. Perfect state transfer and efficient quantum routing: A discrete-time quantum-walk approach. Phys. Rev. A 90, 012331. doi:10.1103/PhysRevA.90.012331
  2. Nitsche, T., Elster, F., Novotný, J., Gábris, A., Jex, I., Barkhofen, S., Christine Silberhorn, 2016. Quantum walks with dynamical control: graph engineering, initial state preparation and state transfer. New J. Phys. 18, 063017. doi:10.1088/1367-2630/18/6/063017