Continuous-Variable Integrated Quantum Optics
Continuous-variable quantum optics is a relatively unexplored field in integrated quantum optics. A small number of experiments have shown the production of quantum states in such devices, but further operations or the production of more advanced states on-chip have not yet been demonstrated. The expertise and facilities available at Paderborn University provide a platform for advancing this field by producing continuous-variable states of high strength and purity.
Integrated Quantum Optics Devices
Integrated devices provide a phase-stable platform for the interaction and manipulation of one or multiple quantum states by combining many non-linear and linear elements into a single device. Recent devices have begun to truly demonstrate the power and versatility of these integrated devices, in which multiple nonlinear interaction regions as well as linear elements and controllable phase shifters have been realized [1].
Most of these devices operate in the single photon regime, which is to say that they operate on the principle of single photon detection. This regime of quantum optics is also known as discrete variable quantum optics. This is named as such because the system has a limited number of possible states, for example, the presence of a single photon or no photon. Single photon quantum optics is relatively insensitive to loss but more complicated states can be very difficult to produce, and detection on the single photon level can be costly.
In contrast, continuous-variable quantum optical states are sensitive to loss but provide other benefits such as cheaper, more efficient detection methods and relative ease in producing more exotic states. As the name suggests, in such systems the quantum state of interest is capable of taking on a continuum of values.
Optical Squeezing
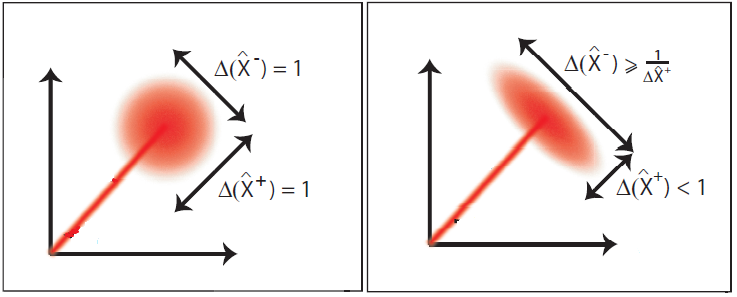
The fundamental resource for continuous-variable quantum optics is optical squeezing. The electric field can be expressed in terms of quadrature operators, Hermitian operators that describe properties of the electric field that can be observed in the lab. These operators, often labelled as the amplitude (X+) and the phase quadrature (X-) operators, do not commute and therefore there is an uncertainty relationship between the two:
where Δ signifies the standard deviation of the observables. For a perfect laser field (with no excess noise) this is a strict equality and the uncertainty in both the amplitude and the phase quadratures is equal. This state is known as a coherent state. In a squeezed state, the uncertainty of one of these observables is less than what it is in the coherent state, at the cost of having increased noise in the other quadrature. This is illustrated in Figure 1 where the ball-on-stick figure of these states (or the phase space representation) is illustrated. This reduction in uncertainty is due to strong correlations between optical sidebands, and is the building block for more advanced quantum optical states in the continuous-wave regime.
Loss
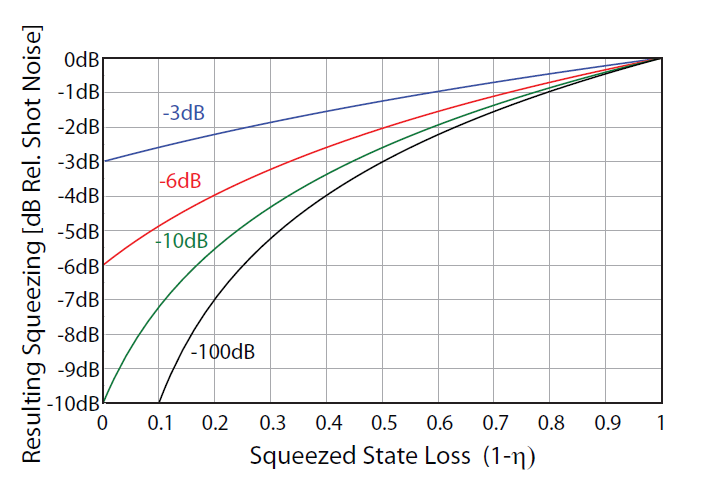
It was noted previously that continuous-variable states are sensitive to loss. This is illustrated in Figure 2. From the figure it is clear that the amount of squeezing available from these states is affected by the amount of loss that the state has undergone. The most squeezing directly measured to date is 12.7dB [2] and as such, 100dB represent near infinite levels of squeezing.
It is therefore paramount in continuous-variable quantum optics devices that loss is minimized. Our group has recently demonstrated losses as low as 0.03dB/cm [3] in a nonlinear quantum device. These low losses are approaching the levels that free-space devices are capable of and as such we expect that we can now produce high levels of pure squeezing in integrated devices and lay the foundation for more advanced manipulation and interaction of continuous-variable quantum optics in integrated devices.
References:
[1] J. W. Silverstone, D. Bonneau, K. Ohira, N. Suzuki, H. Yoshida, N. Lizuka, M. Ezaki, C. M. Natarajan, M. G. Tanner, R. H. Hadfield, V. Zwiller, G. D. Marshall, J. G. Rarity, J. L. O’Brien and M. G. Thompson, “On-chip quantum interference between silicon photon-pair sources” Nature Photon. 8, 104-108, (2013).
[2] T. Eberle, S. Steinlechner, J. Bauchrowitz, V. Händchen, H. Vahlbruch, M. Mehmet, H. Müller-Ebhardt, and R. Schnabel. “Quantum enhancement of the zero-area Sagnac interferometer topology for gravitational wave detection“ Phys. Rev. Lett. 104, 251102 (2010).
[3] K-H. Luo, H. Herrmann, S. Krapick, R. Ricken, V. Quiring, H. Suche, W. Sohler, and C. Silberhorn “Two-color narrowband photon pair source with high brightness based on clustering in a monolithic waveguide resonator.” arXiv, 1306.1756v1 [quant-ph] (2013).