Quantum walks on percolation graphs

Quantum walks turned out to be a promising canditate for analysing universal transport phenomena. Randomness  -- and in particular percolation [1]-- is essential for capturing various effects known from observations in biological, statistical and condensed matter physics.

In the standard percolation model, which is extensively studied in mathematics and physics,  links between vertices of a finite graph are present or absent only with a certain probability p.

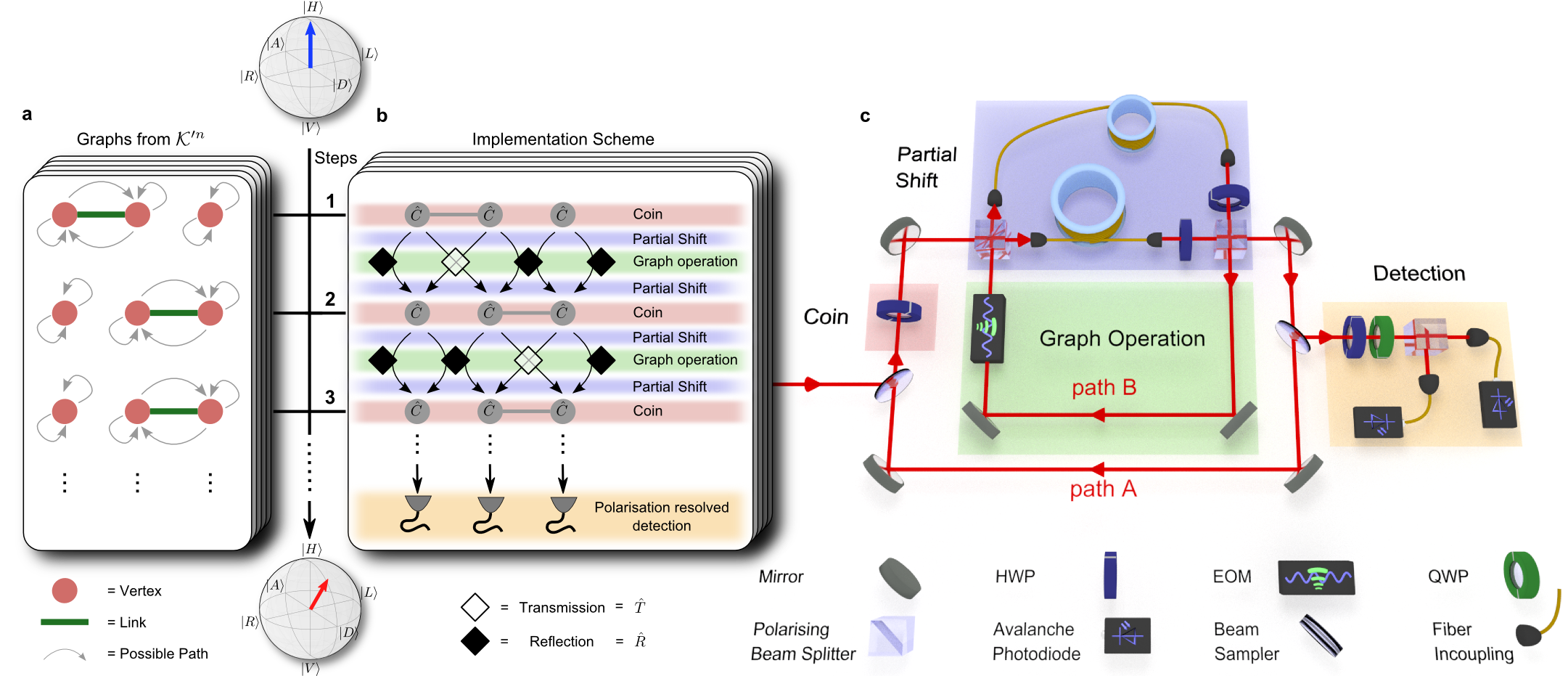
We have demonstrated a quantum walk evolution on a dynamical percolation graph with 3 vertices. In order to do that we have to dynamically cut the link between potential walker positions going beyond the quantum walk systems on static graphs as presented before.

 Though we implement a one-dimensional walk we use the setup originally designed for the 2d-walk as presented in video 3 and figure 1c, but now  the pulses alternate between the two paths A and B.

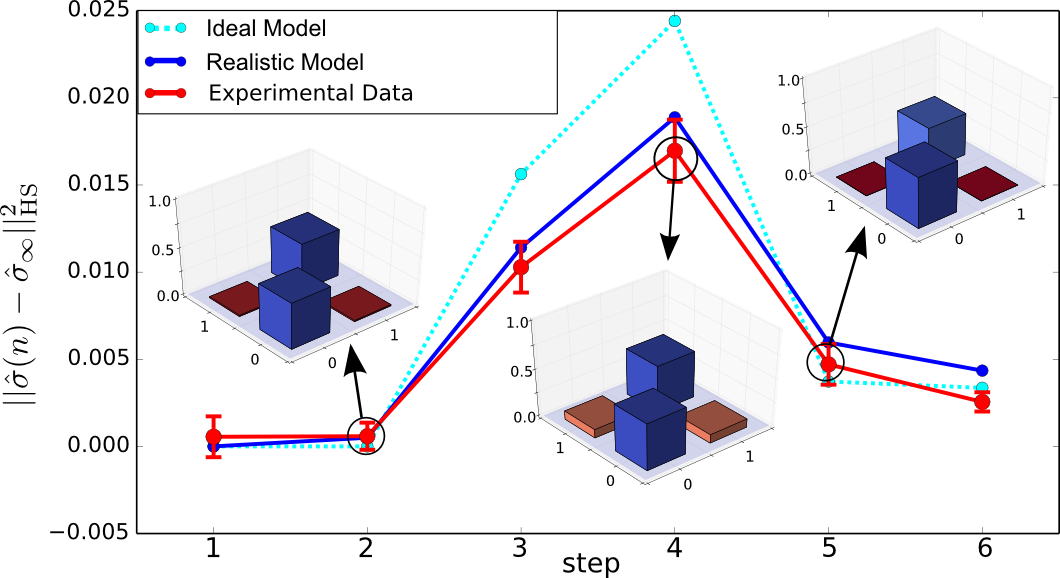
Figure 1: a) One pattern of a dynamically changing graph with 3 sites used in the experiment (shown explicitly for 3 steps). The input coin state (blue arrow) is evolved (red arrow) and measured tomographically at every step. b) Implementation scheme of the exemplary graph, the reflection and transmission operators are represented by filled and hollow diamonds, respectively. c) Setup scheme of the time-multiplexed Percolation QW. According to the implementation scheme the walker always alternates between paths A and B. The colour coding is used to mark corresponding entities in both panels. We average over 64 different graph structures to realise the 50% link probability. Bild vergrößern

Path A contains a waveplate realizing the coin operation as explained above. In the next roundtrip the pulses travel through path B with an EOM implementing the graph operation, which means that depending on the switch of the EOM a transmission operation (for a present link in the graph) or a reflection operation (for a broken link) is performed, see figure 1b. With such a double step scheme we are able to realize finite or percolation graphs (see figure 1a) just by reprogramming the corresponding EOM switching schemes. Exploiting these new abilities of a graph modification we investigate the coherence properties of a quantum walk on a graph comprising 3 vertices and links with a 50% probability of being present. For this example we reconstructed the full density matrix of the coin state of the walker and compared it with the totally mixed state, a state which does not contain any coherence anymore, see fig. 2.

Figure 2 :Hilbert--Schmidt distance between the maximally mixed (= fully decoherent state) and measured data (red), ideal model (turquoise), and realistic model (blue). The insets show the experimental density matrix for the three chosen steps. Bild vergrößern

The observed density matrix becomes completely mixed in step 1 (distance = 0),but surprisingly the distance increases again. Such a revival from the completely mixed state is the witness that between the position and the coin degree of freedoms sufficient coherence survives the averaging over all patterns reflecting a non-Markovian behaviour.  This increase (and decrease)of coherence is also reflected in the non-zero off-diagonal elements of the density matrices which are shown as insets in figure 2. All the detail about these measurement can be found in [2].

 

References:

  1. Kollár, Bálint, et al. "Asymptotic dynamics of coined quantum walks on percolation graphs." Physical review letters 108.23 (2012): 230505.
  2. Elster, F., Barkhofen, S., Nitsche, T., Novotný, J., Gábris, A., Jex, I., Silberhorn, C., 2015. Quantum walk coherences on a dynamical percolation graph. Scientific Reports 5, 13495. doi:10.1038/srep13495