Quantum Walks
Quantum walks describe the coherent propagation of quantum particles in networks. Thisversatile concept allows one to explain the complex quantum dynamics in open and closedphysical, chemical, and biological systems. Additionally, quantum walks provide a new andpromising framework for applications in quantum information processing. Our group’s workfocuses on implementing novel forms of quantum walks in cutting-edge optical architectures, ranging from fiber-based experiments to integrated wave guide arrays, for studying the walk’squantum features. This research is funded through the ERC project QuPoPCoRN.
The quantum walk principle
The research on quantum walks is inspired by the versatility of its classical counterpart, the classical random walk. Random walks are used for example to explain physical effects like the Brownian motion, or as a basic framework for search algorithms or even for predictions of the price evolution at the stock market. Motivated by the diverse applications research is now focusing on phenomena and algorithms, that rely on and even benefit from of the underlying quantum mechanics in quantum walks. A nice example hereby are coherent procedures in nature, like the energy transport in photosynthesis.
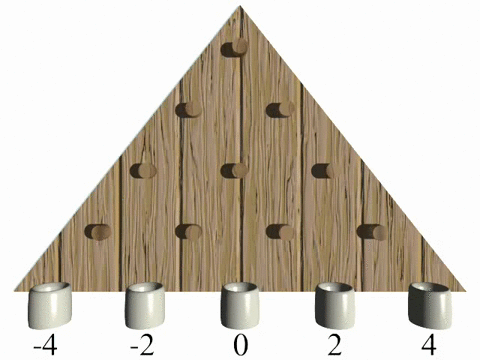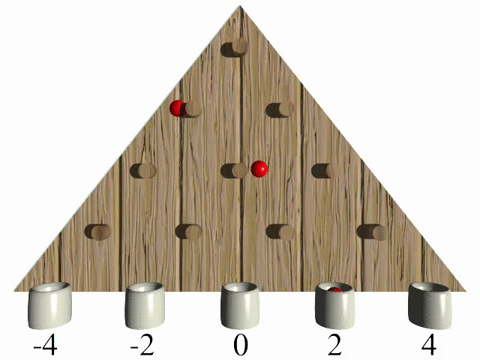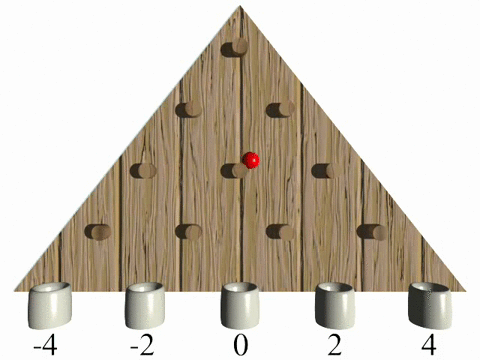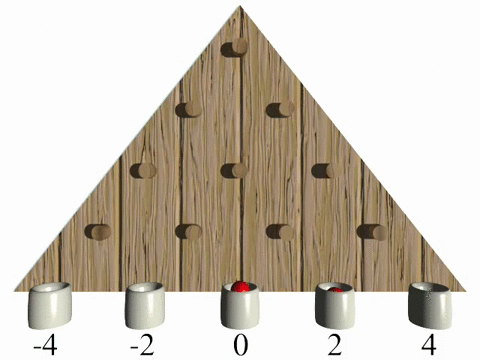
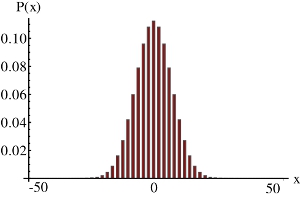
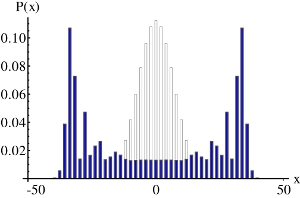
In a classical random walk a walker decides randomly (by tossing a coin), which path he is going to use, which can be visualized as a simple Galton board experiment (Vid. 1). After a discrete number of steps the probability to end up at a specific final position is given by a binomial distribution with a spread propotional to the square root of steps (rows).
In contrast a quantum walker is described by a quantum mechanical wave function. During the evolution the wave function spreads over different positions, leaving the system in a coherent superposition of all possible paths. This results in quantum interference effects, which drastically change the final probability distribution (Vid. 2). One significant difference of the two models is a quadratically faster spread in a quantum walk, reducing the average time to reach distant locations. The evolution in a quantum walk is, as opposed to the classical random walk, fully deterministic with the final distribution being highly dependent on the environmental conditions.
In general you can distinguish between two different forms of quantum walks, the discrete-time quantum walk and the continuous-time quantum walk, which are both investigated in our group.
Quantum walks with dynamical control: graph engineering, initial state preparation and state transfer
Dynamically influencing the walker’s evolution gives a high degree of flexibility for studying various applications. Additionally to the described applications for Anderson localization and percolation we realised time-multiplexed finite quantum walks of variable size, the preparation of non-localised input states and their dynamical evolution. As a further application, we implement a state transfer scheme for an arbitrary input state to two different output modes.
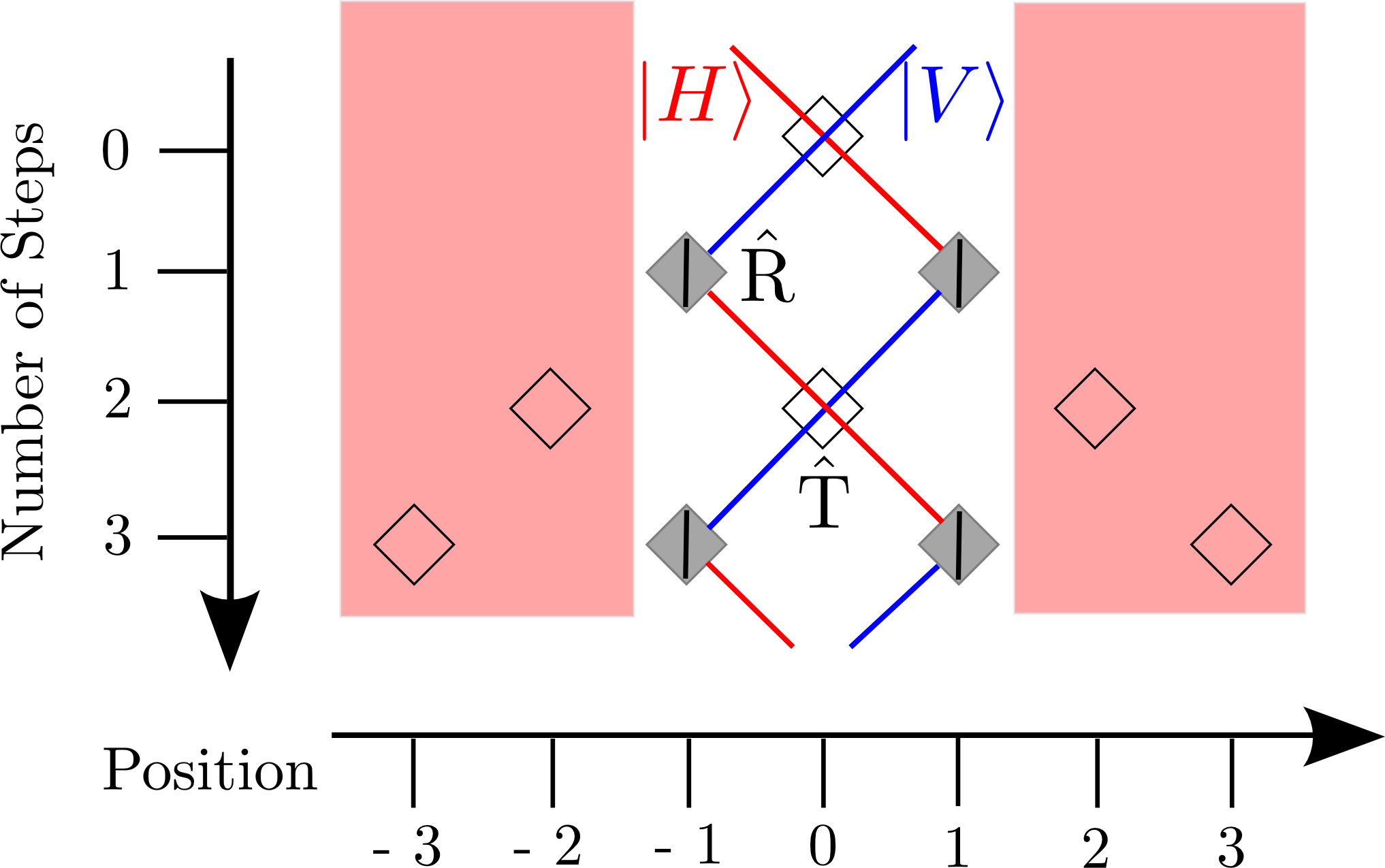
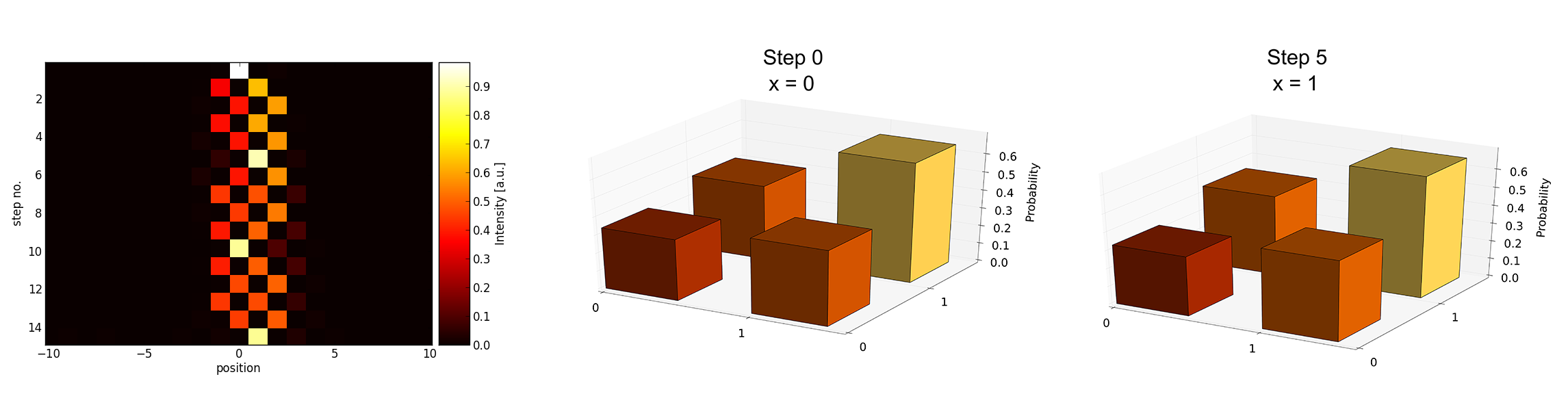
First, we vary the size of the underlying graph by introducing corresponding reflection operations with the EOM as illustrated in fig. 1.
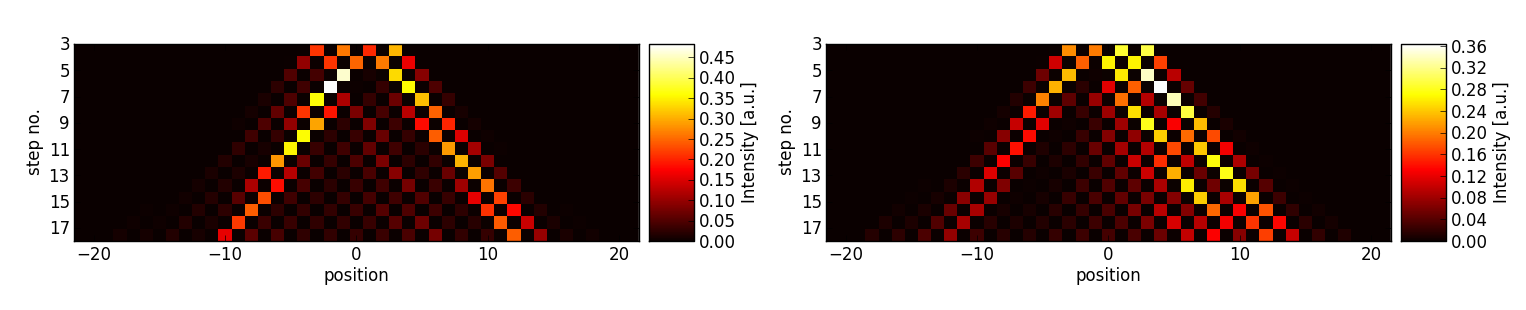
The timing of the reflection switching consequently determines how large the graph is and thus how far the walker’s wavefunction is spread out. Three examples for finite graphs in contrast to an unlimited walk are presented in figure 2.
In figure 2a, we observe an additional interesting feature of the walk on a finite graph: The walker, initially spread out, is not only reflected at the boundaries, but even exhibits revival (within experimental errors) at the initial position 0 in step 10.
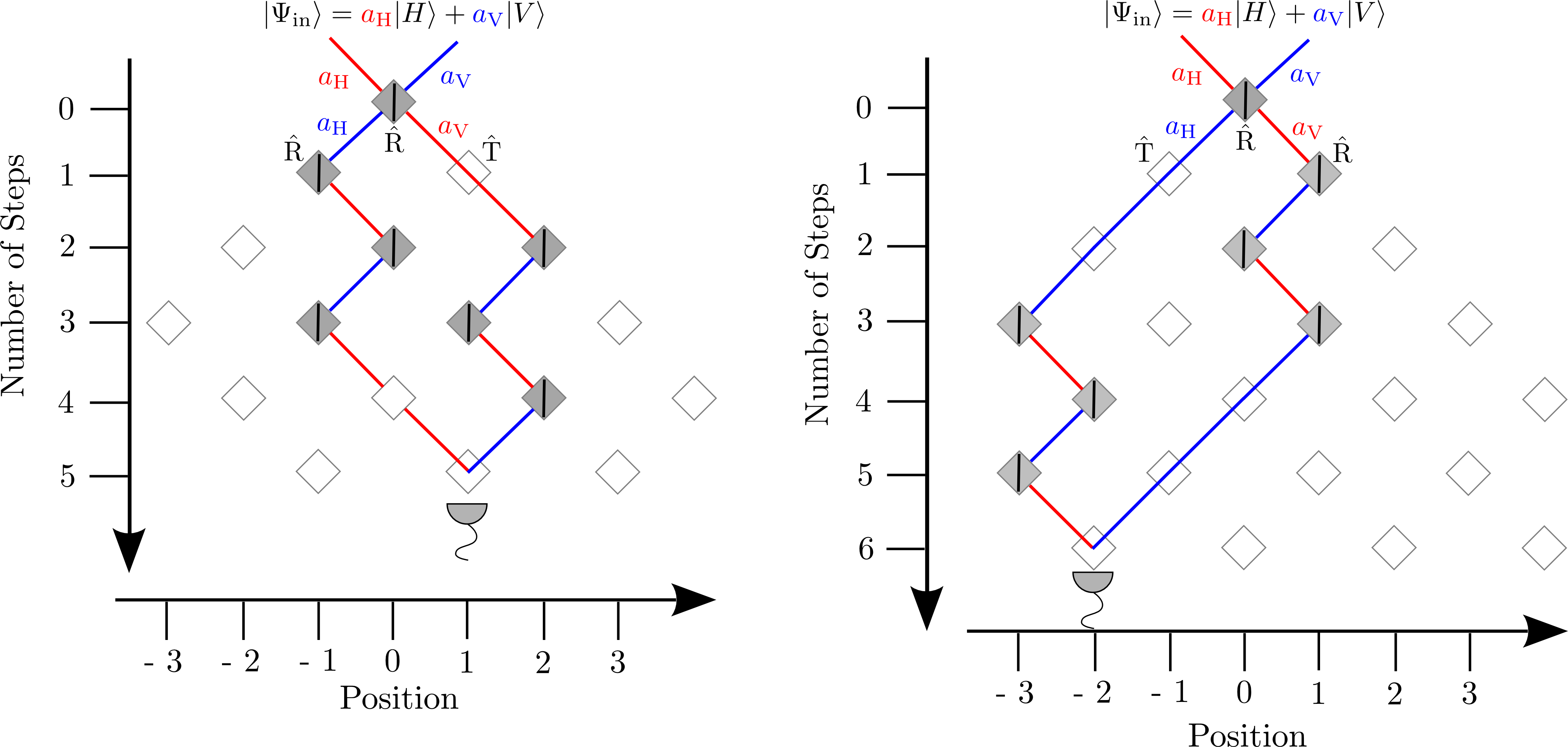
Most quantum walk experiments including those presented above are performed with localised input states. However, there are theory proposals, e.g. for boson sampling in a time-multiplexing setup or for quantum search, which rely on initial states occupying several positions. The ''in-situ'' state preparation, i.e. the preparation of different initial states within the quantum walk setup, guarantees phase-stable pulse trains with controlled polarization inherently exhibiting a coherent evolution. Two examples of transformations accessible by the EOM used in the present setup are illustrated in Figure 3. We use these schemes to prepare two states with four positions, but different polarizations.
For these given input states, we observe the evolution in a balanced walk on an infinite graph (see Fig. 4). The comparison of the two cases reveals the relevance of the input polarisation: For the | VVHH> state, the walker evolves along two branches which are more distinctively defined than for the | VHVH>state. Here in comparison, especially the right branch is much more smeared out leading to a very different intensity distribution in position space. By reprogramming the EOM switching patterns, the preparation of well-defined input states distributed over a higher number of positions is possible as well.
Zhan et al. in [1] proposed a state transfer scheme via discrete time quantum walks. The possibility of dynamical coin control allows for the easy implementation of this protocol in our setup. We are able to observe a revival of the walker's initial polarisation state at a chosen position, although it is beforehand spread out in space and undergoes switchings in polarization. Different protocols transferring the state to different positions can be realised simply by reprogramming the EOM. In figure 5, we show the implementation of 2 exemplary non-trivial schemes.
All the presented experiments rely on the full dynamical control of the time-multiplexed quantum walk, which includes adjustable coin operation as well as the possibility to flexibly configure the underlying graph structures. Details about the presented applications as well as a thorough explanation of all the experimental challenges and pitfalls including a full analysis of the EOM features, timings and loss handling are published in [2].
References:
- Zhan, X., Qin, H., Bian, Z., Li, J., Xue, P., 2014. Perfect state transfer and efficient quantum routing: A discrete-time quantum-walk approach. Phys. Rev. A 90, 012331. doi:10.1103/PhysRevA.90.012331
- Nitsche, T., Elster, F., Novotný, J., Gábris, A., Jex, I., Barkhofen, S., Christine Silberhorn, 2016. Quantum walks with dynamical control: graph engineering, initial state preparation and state transfer. New J. Phys. 18, 063017. doi:10.1088/1367-2630/18/6/063017
Quantum walks on percolation graphs
Quantum walks turned out to be a promising canditate for analysing universal transport phenomena. Randomness -- and in particular percolation [3]-- is essential for capturing various effects known from observations in biological, statistical and condensed matter physics.
In the standard percolation model, which is extensively studied in mathematics and physics, links between vertices of a finite graph are present or absent only with a certain probability p.
We have demonstrated a quantum walk evolution on a dynamical percolation graph with 3 vertices. In order to do that we have to dynamically cut the link between potential walker positions going beyond the quantum walk systems on static graphs as presented before.
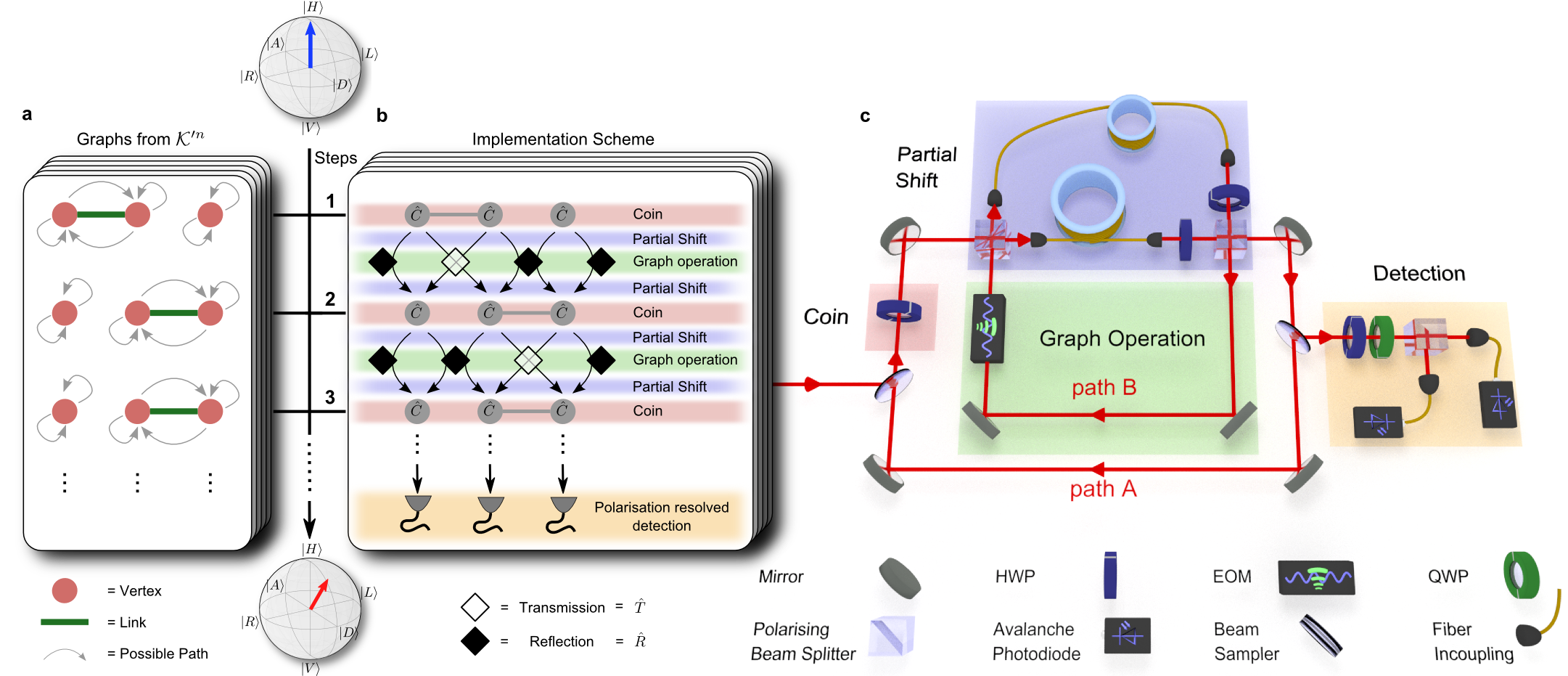
Though we implement a one-dimensional walk we use the setup originally designed for the 2d-walk as presented in video 3 and figure 1c, but now the pulses alternate between the two paths A and B.
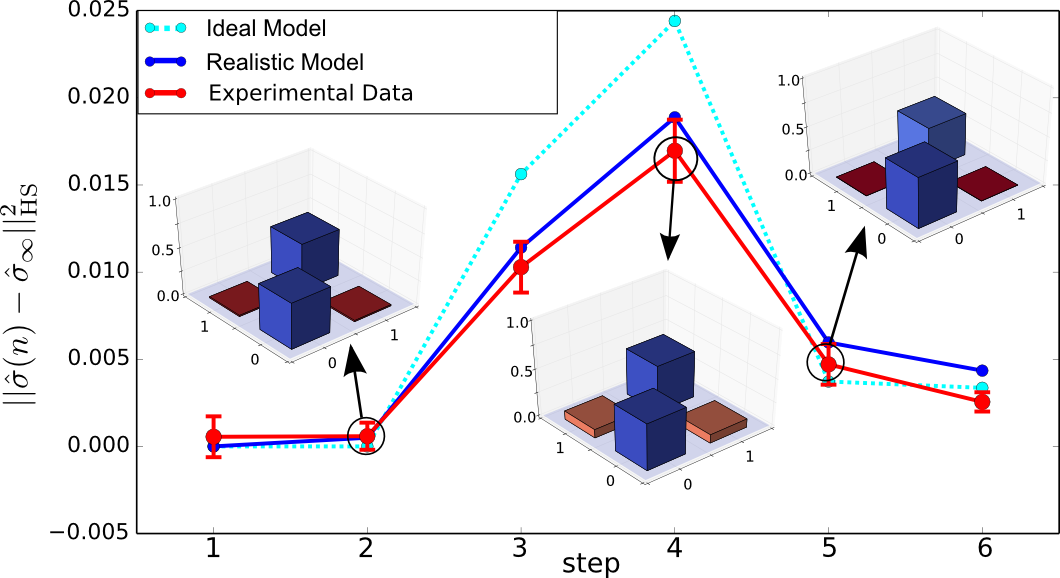
Path A contains a waveplate realizing the coin operation as explained above. In the next roundtrip the pulses travel through path B with an EOM implementing the graph operation, which means that depending on the switch of the EOM a transmission operation (for a present link in the graph) or a reflection operation (for a broken link) is performed, see figure 1b. With such a double step scheme we are able to realize finite or percolation graphs (see figure 1a) just by reprogramming the corresponding EOM switching schemes. Exploiting these new abilities of a graph modification we investigate the coherence properties of a quantum walk on a graph comprising 3 vertices and links with a 50% probability of being present. For this example we reconstructed the full density matrix of the coin state of the walker and compared it with the totally mixed state, a state which does not contain any coherence anymore, see fig. 2.
The observed density matrix becomes completely mixed in step 1 (distance = 0),but surprisingly the distance increases again. Such a revival from the completely mixed state is the witness that between the position and the coin degree of freedoms sufficient coherence survives the averaging over all patterns reflecting a non-Markovian behaviour. This increase (and decrease)of coherence is also reflected in the non-zero off-diagonal elements of the density matrices which are shown as insets in figure 2. All the detail about these measurement can be found in [4].
References:
3. Kollár, Bálint, et al. "Asymptotic dynamics of coined quantum walks on percolation graphs." Physical review letters 108.23 (2012): 230505.
4. Elster, F., Barkhofen, S., Nitsche, T., Novotný, J., Gábris, A., Jex, I., Silberhorn, C., 2015. Quantum walk coherences on a dynamical percolation graph. Scientific Reports 5, 13495. doi:10.1038/srep13495
Discrete-time quantum walk in two dimensions
In anology to the 1D experiments we implemented quantum walks on a 2D lattice [5] using the time-multiplexing method (Vid.3).
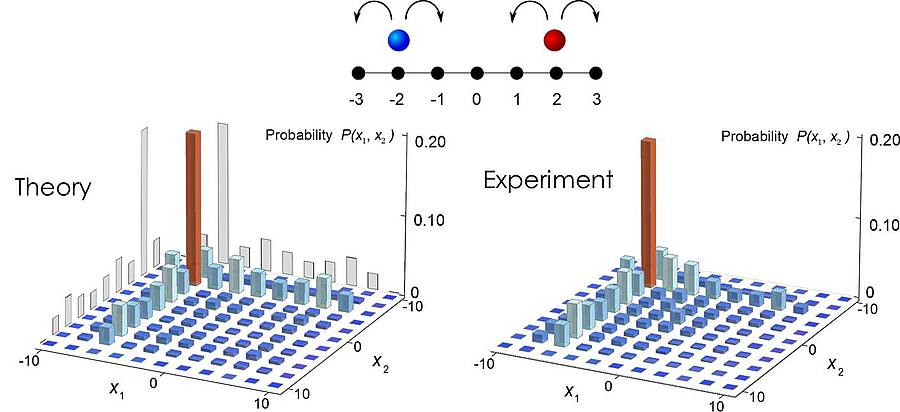
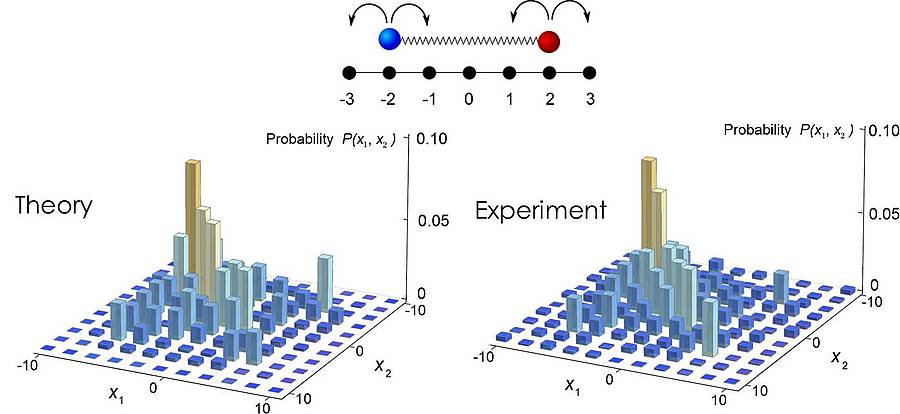
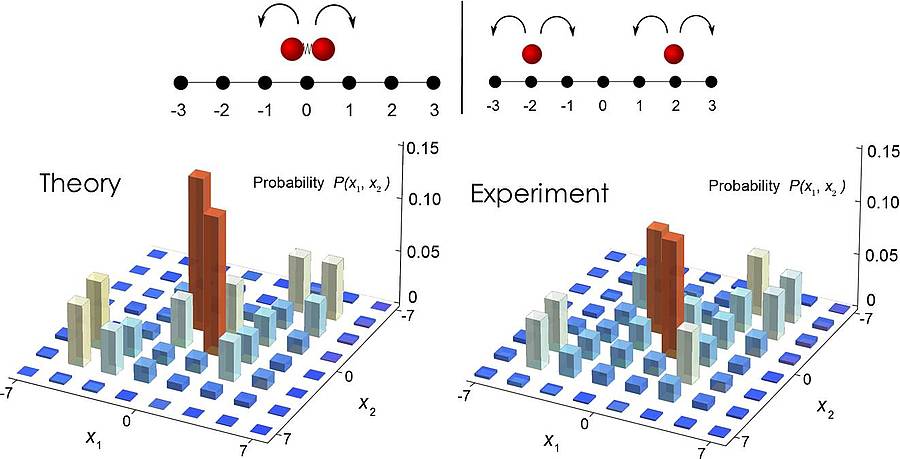
The scenario of one particle propagating on a 2D lattice can directly be translated to a quantum walk with two particles on a single line. Hence, by choosing different quantum coins we could mimic the dynamics of particles with different kinds of interactions (Fig.3).
An interesting effect occurs in quantum walks of two indistinguishable bosons scattering at each other. This leads to the creation of a bound state, which forces the particles to stick together during their propagation (Fig. 4).
Discrete-time quantum walk in one dimension
In a discrete-time quantum walk the evolution is split into two operations, similar to the CRW. First the walker "tosses a quantum coin" and according to the outcome he steps either to the left or the right, when walking on a one-dimensional line. Both operations occur at a discrete point in time.
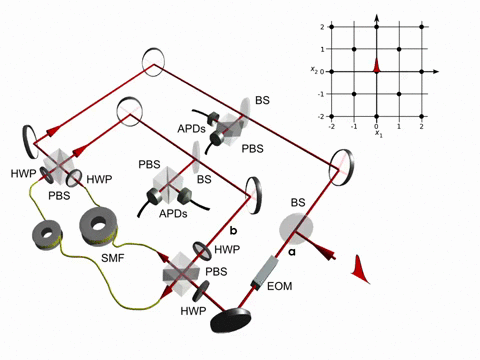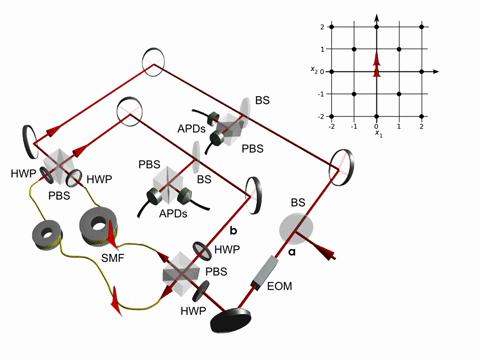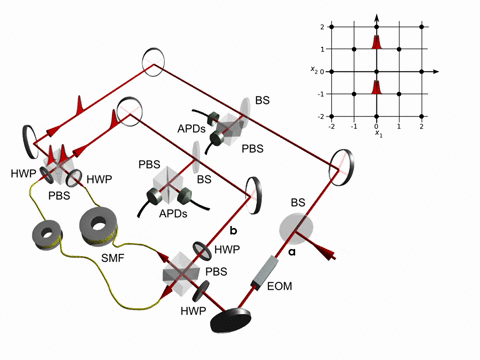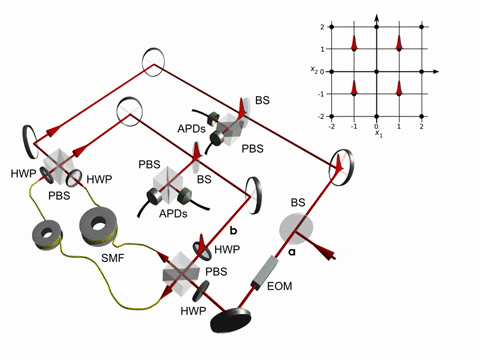
We implemented a discrete-time quantum walk in a fiber loop system [6,7] using a time-multiplexing technique (Fig. 1). In the experiment photons travel a longer or a shorter fiber depending on their polarization state, which corresponds to a step to the left or the right.
Continuous-time quantum walk
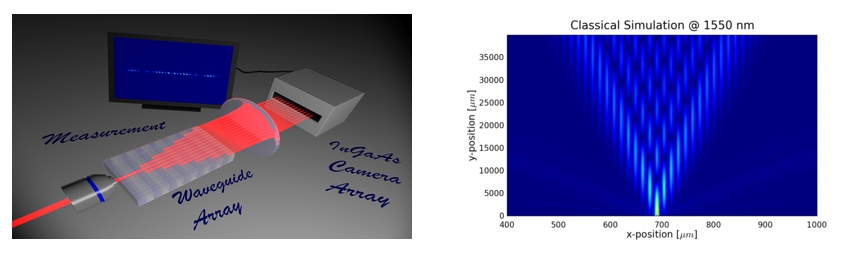
In a continuous-time quantum walk the coin and step can not be separated from each other but rather happen simultaneously for example during the propagation through an array of waveguides (Fig. 5).
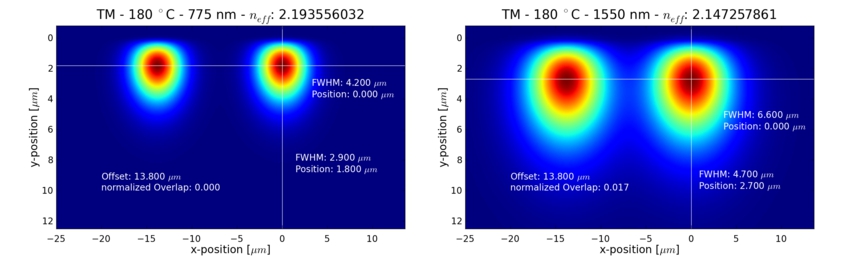
We are working on a realization of a continuous-time quantum walk based on an array of coupled waveguides on a periodically poled LiNbO3 crystal. In this array single photons of a certain wavelength can coherently couple from one waveguide to its next neighbors due to a non vanishing evanescent field overlap into the neighboring channels (Fig. 6). By varying the distance between the channels it is possible to engineer the coupling strength of the device. Additionally to the linear coupling our devices support the intrinsic generation of photon pairs right inside the array by driving a parametric downconversion process. The phase matching condition is provided by the periodic poling of the LiNbO3 crystal and can be fine tuned by the operating temperature of the device. For this scheme a classical pump field is injected into one channel of the waveguide array and somewhere along this array a photon pair is created, which is the starting point for a two-walker continuous-time quantum walk. Through temperature tuning it is possible to go from the degenerate to the non-degenerate regime of the PDC process by changing the phase matching condition.
Production of Samples
As all needed production steps from the bare LiNbO3 Waver to the finished waveguide array sample can be performed in our own clean room facilities we have the opportunity to engineer our waveguide arrays exactly to fit our demands. The waveguide arrays are produced by indiffusion of photolithographically prepared strips of titanium into the LiNbO3 crystal. We are constantly working to improve the quality of our samples to provide the homogeneity needed for our experiments.
By controlling the environmental conditions we were able to simulate the dynamics of quantum particles traversing a homogeneous system influenced by a tunable source of decoherence. This allowed for a controlled transistion between the coherent quantum mechanical world to a classical environment where the distribution is determined by randomness. Furthermore we showed that photons travelling through a disordered system could get trapped, a phenomenon theoretically investigated by P. W. Anderson over 50 years ago [8].
References
5. A 2D Quantum Walk Simulation of Two-Particle Dynamics
A. Schreiber, A. Gábris, P. P. Rohde, K. Laiho, M. Stefanak, V. Potocek, C. Hamilton, I. Jex, Ch. Silberhorn
6. Photons Walking the Line: A Quantum Walk with Adjustable Coin Operation
A. Schreiber, K.N. Cassemiro, V. Potocek, A. Gábris, P. J. Mosley, E. Andersson, I. Jex and Ch. Silberhorn
[PDF, Phys. Rev. Lett. 104, 050502 (2010)]
7. Decoherence and Disorder in Quantum Walks: From Ballistic Spread to Localization
A. Schreiber, K. N. Cassemiro, V. Potocek, A. Gábris, I. Jex and Ch. Silberhon
[PDF,
Phys. Rev. Lett. 106, 180403 (2011)]
8. Absence of Diffusion in Certain Random Lattices
P.W. Anderson

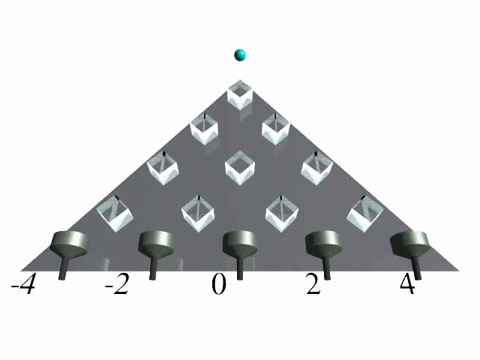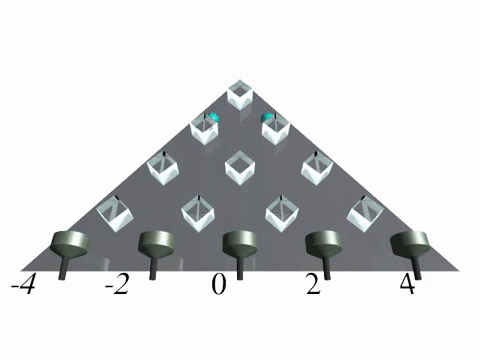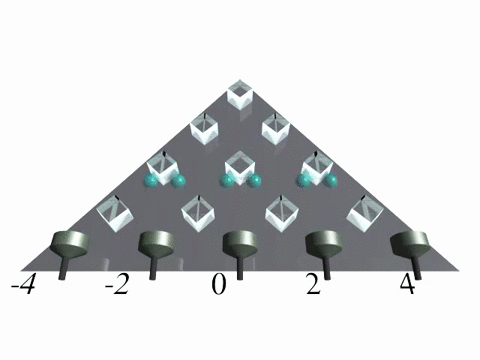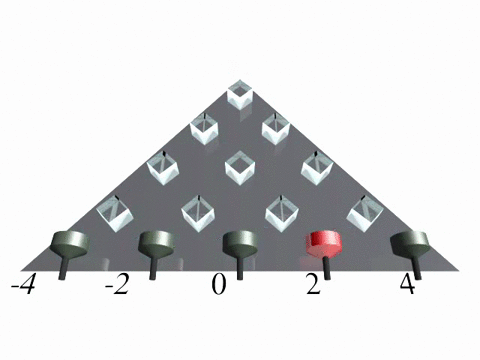


![Discrete-time quantum walk Figure 1: Experimental implementation of a discrete-time quantum walk on a line using a time-multiplexed system. For details see [1,2].](/fileadmin-nw/physik/Arbeitsgruppen/integrierte-quantenoptik/img/quantumwalks_fig1_discretetimeqw.jpg)