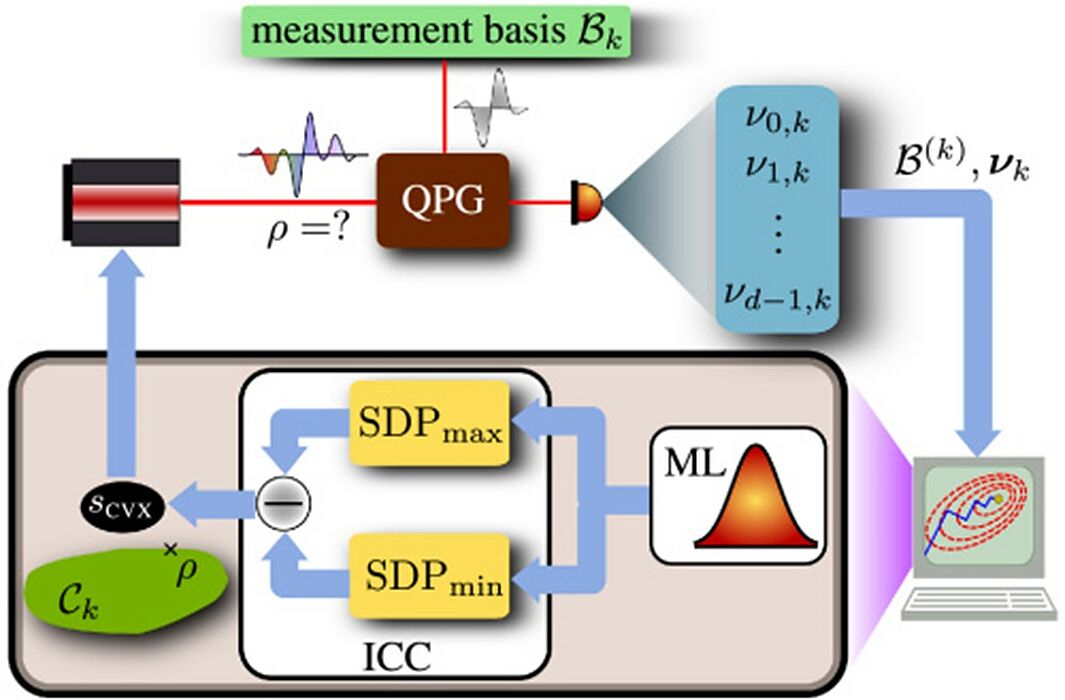
Performing quantum state tomography is a key challenge for quantum information technologies. Usual scan tomography techniques are slow and require a prohibitively large number of measurement settings. Compressive sensing techniques can alleviate the situation but require a priori knowledge about the unknown state – a logical conundrum. We adapt ideas from compressive sensing and implement an adaptive compressive tomography scheme that requires no a-priori knowledge of the state under investigation to perform a full tomography of few-photon states in the time-frequency domain. The results are immediately applicable to single-photon level as well as squeezed states.
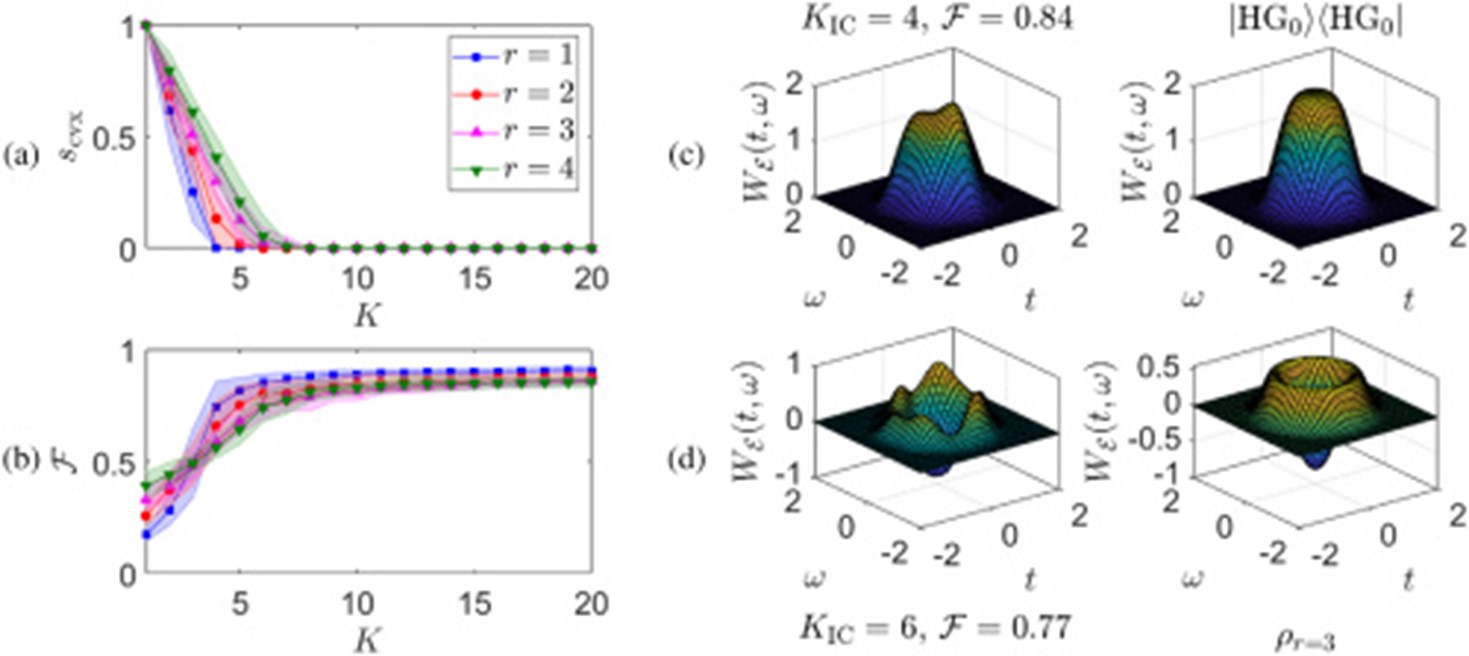
We use the quantum pulse gate to project the input state onto random temporal mode distributions that feed the compressive tomography algorithm and reconstruct the original state. We report reconstructed states with fidelities above 80% for both temporal modes and frequency bin states in time-frequency spaces of dimension up to 60. The reconstruction took only around 20 measurements per dimension d of the space measurements, where naïve approaches require a number of measurements in the order of (d+1)^2.
Our results open a promising avenue towards the efficient characterization of large quantum states, which will form the cornerstones of future quantum technologies.
Universal compressive tomography in the time-frequency domain, Jano Gil-Lopez, Yong Siah Teo, Syamsundar De, Benjamin Brecht, Hyunseok Jeong, Christine Silberhorn, and Luis L. Sánchez-Soto, Optica 8(10), 1288-1289 (2021).